Let’s define a function first before delving into the concept of a horizontal asymptote. A function is an equation that shows the relationship between two things. Functions typically explain how y is related to x. To provide a visual representation, functions are frequently graphed. A horizontal asymptote is a straight line that shows how a function behaves at the graph’s extreme edges. A horizontal asymptote, on the other hand, is forbidden territory. The function can approach and even cross the asymptote. Horizontal asymptotes occur for polynomial numerators and denominators. These are referred to as rational expressions.

The horizontal asymptote of a function is a horizontal line with which the function’s graph appears to coincide but does not truly coincide. The function’s final behavior is identified by the horizontal asymptote. This asymptote is discussed in this article. So, please continue reading to learn more about it.
Horizontal Asymptote rules
Determine the degrees of a rational function’s numerator (n) and denominator (d) to determine its horizontal asymptote (d).
- If n is smaller than d, HA equals y = 0.
- Then, if n is more than d, there is no HA.
- If n = d, HA equals y = leading coefficient ratio.
The horizontal asymptote of an exponential function of the form f(x) = abkx+c is y = c.
A horizontal asymptote cannot exist for a polynomial function (such as f(x) = x+3, f(x) = x^2-2x+3, and so on) since the limits of these functions as x trend to or – do not produce real integers.
To get the horizontal asymptote of any arbitrary function other than these, we simply apply limits as x goes to infinity and x – infinity.
Horizontal Asymptote rules rational function
There can only be one horizontal asymptote for a rational function. Though we can use the limits to find the HAs, the following methods are more convenient for locating the horizontal asymptotes of rational functions:
- The function has no HA if the degree of the numerator is greater than the degree of the denominator.
- The function has one HA, which is y = 0, if the degree of the denominator is greater than the degree of the numerator.
- If the numerator’s degree equals the denominator’s degree, the function has one HA, which is y = the ratio of the leading coefficients in the numerator and denominator.
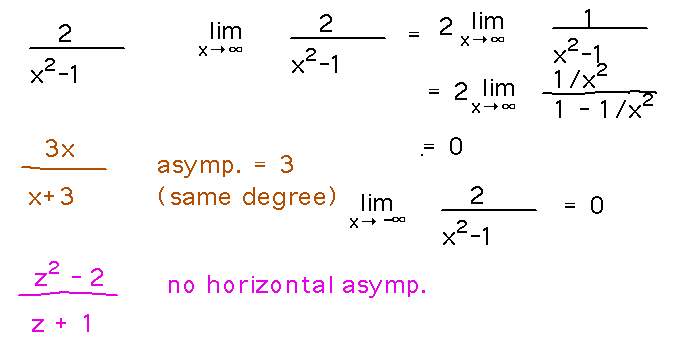
In the preceding section’s example (where f(x) = 2x / (x – 3)), the numerator’s degree equals the denominator’s degree (= 1). As a result, the HA of f(x) is y = 2/1 = 2. It’s worth noting that we got the same result even when we applied the constraints. Here are a few more examples.
- y = (x2+3) / (2x) has no HA.
- HA of y = (2x) / (x2 + 3) is y = 0.
- HA of y = (2×2) / (x2 + 3) is y = 2.
Horizontal Asymptote rules example 1
Determine the horizontal asymptote of each rational function:
f(x) = 4x^2 – 5x/ x^2 – 2x +1
First, the degrees of the polynomials must be compared. Both the numerator and denominator are second degree polynomials. The coefficients of the highest terms must be divided because they are of the same degree.
The coefficient of the highest term in the numerator is 4.
The coefficient of the highest term in the denominator is a known 1.
4/1 = 4
At y = 4, the horizontal asymptote is reached.
Horizontal Asymptote rules example 2
f(x) = x^2 – 9/ x+ 10
First, the degrees of the polynomials must be compared. A polynomial of second degree is included in the numerator, while a polynomial of first degree is included in the denominator. Because the polynomial in the numerator has a higher degree than the denominator, there is no horizontal asymptote. Instead, a slant asymptote exists.Read Also: Difference Quotient Calculator: steps, formula, example and more
Horizontal Asymptote rules example 3
f(x) = x – 12/ 2x^3 + 5x – 3
First, the degrees of the polynomials must be compared. In the numerator is a first degree polynomial; while in the denominator is a third degree polynomial. The horizontal asymptote is at y=0 because the polynomial in the numerator has a lower degree than the polynomial in the denominator.
Horizontal Asymptote rules examples
Example 1
Find the horizontal asymptote of y = (3×2+2x)/(x+1).
Solution:
The degree of the numerator in this case is 2.
The denominator’s degree Equals 1.
As a result, the degree of the numerator is greater than the degree of the denominator.
As a result, f(x) has no HA.
Answer: There is no HA in the supplied function.
Example 2
Determine the value of k using the horizontal asymptote rules if the HA of f(x) = 2x – k equals y = 3.
Solution:
We know that the vertical transformation of an exponential function determines its HA.
As a result, the HA of f(x) = 2x – k is y = -k.
However, it is assumed that the HA of f(x) equals y = 3.
As a result, -k = 3 (or) k = -3.
k = -3 is the answer.
Example 3
Determine the horizontal asymptotes of f(x) = x/x2+3.
Solution:
Given that f(x) = x/x2+3,
Because the degree of the numerator is smaller than the degree of the denominator, the horizontal asymptote is placed at y = 0.
Example 4
Determine the horizontal asymptotes of f(x) =(x2+3)/x+1.
Solution:
Given that f(x) = (x2+3)/x+1
As you can see, the numerator has a higher degree than the denominator. As a result, there is no horizontal asymptote.
Horizontal Asymptote rules limits
Horizontal asymptotes and infinity limits are inextricably linked. One cannot exist without the other. If you have a rational function, such as
f(x)=3x-7/2x+8

Identifying the limit at infinity or negative infinity is equivalent to locating the horizontal asymptote.This is what you do. First, take note of the numerator’s degree (the highest power of x in the numerator) and the denominator’s degree. You now have three options:
If the numerator’s degree is greater than the denominator’s degree, for example:
f(x)=6x^4 +x^3 -7/2x^2 +8
There is no horizontal asymptote and no function limit as x approaches infinity (or negative infinity).
If the denominator’s degree is greater than the numerator’s degree, for example:
g(x)= 4x^2 -9/x^3 +12
The x-axis( that’s the line y=0) is the horizontal asymptote and
lim x→∞ g(x)= lim x→∞ g(x)=0
If the degrees of the numerator and denominator are identical, divide the coefficient of the greatest power of x in the numerator by the coefficient of greatest power of x in the denominator. This quotient offers you the solution to the limit issue as well as the height of the asymptote.
For example, if h(x)= 4x^3 -10x +1 /5x^3 +2x^2 -x ,lim x→∞ (xh)= lim x→∞ h(x)=⅘, and h has a horizontal asymptote at y=⅘.
Keep in mind that substitution may not always work for cases with infinite bounds.
If you try plugging infinity into x in any of the rational functions in the preceding list, you get infinity by infinity.
However, this does not equal one. (By the way, infinite minus infinity does not equal zero.)
Keep in mind that a result of ∞/∞ or (∞-∞) tells you nothing about the answer to a limit problem.
Example
Find the horizontal asymptote(s) of f(x)=3x+7/2x−5.
| lim x→∞ 3x+7/2x – 5
=lim x→∞ 3x+7/x /2-5/x =3+0/2-0 =3/2 |
First, when x approaches positive infinity, we determine the limit. |
| lim x→∞ 3x+7/2x – 5
=lim x→∞ 3x+7/x /2-5/x =3+0/2-0 =3/2 |
And we get the limit when x approaches negative infinity. |
| Therefore, the function has horizontal asymptote
y=3/2 |
Because the two limits were equal, this function has a single horizontal asymptote. Because asymptotes are lines, they are described by equations rather than numbers. |
Horizontal Asymptote rules degree
While vertical asymptotes explain a graph’s behavior as the output becomes extremely big or very tiny, horizontal asymptotes help describe a graph’s behavior when the input becomes very large or very small. Remember that the end behavior of a polynomial will be the same as the leading term. Similarly, the end behavior of a rational function will be the same as the ratio of the leading terms of the numerator and denominator functions.
When looking for horizontal asymptotes, there are three possible outcomes:
- The function has no HA if the degree of the numerator is greater than the degree of the denominator.
if: degree of numerator greater than degree of denominator
then: horizontal asymptote: none.
- The function has one HA, which is y = 0, if the degree of the denominator is greater than the degree of the numerator.
if: degree of numerator less than degree of denominator
then: horizontal asymptote: y = 0 (x-axis).

- If the numerator’s degree equals the denominator’s degree, the function has one HA, which is y = the ratio of the leading coefficients in the numerator and denominator.
if: degree of numerator = degree of denominator
then: horizontal asymptote: y = leading coefficient of numerator/ leading coefficient of denominator.
Horizontal Asymptote rules calculus
The line, y = L is a horizontal asymptote of the curve y = f(x), if either
lim x→∞ f(x) =L or,
lim x→ – ∞ f(x) = L
Then,
For the rational function, f(x)
The horizontal asymptote is y = 0 if the degree of x in the numerator is smaller than the degree of x in the denominator. If the degree of x in the denominator equals the degree of x in the numerator, then y = c, where c is obtained by dividing the leading coefficients.
Example
Find the function’s horizontal and vertical asymptotes, for example.
f(x) =2x+1/ 3x-5
Solution:
Divide x by the numerator and denominator.
lim x→∞ 2x+1 / 3x-5
= lim x→∞ 2+1/x / 3-5/x
Then, = lim x→∞ (2+1/x) / lim x→∞ (3-5/x)
= lim x→∞ 2+lim x→∞ 1/x / lim x→∞ 3-5 lim x→∞ 1/x
=2+0/3-5(0)
=2/3
The horizontal asymptote is the line y=2/3.
Method two:
The numerator’s degree of x equals the denominator’s degree of x.
By dividing the leading coefficients, we obtain ⅔.
The line y=⅔ represents the horizontal asymptote.
Horizontal Asymptote rules exponential function
Variables can be exponents. Variable exponents obey all of the exponent characteristics given in Properties of Exponents.
Horizontal Asymptote rules graph 1
An exponential function is one that has a changeable exponent. Exponential functions include f (x) = 2x and g(x) = 53x. We can draw graphs of exponential functions. The graph of f (x) = 2x is as follows:
f (x) = 2x
Because 2x greater than 0 for every x, the graph exhibits a horizontal asymptote at y = 0. It runs through the point (0, 1).
Horizontal Asymptote rules Graph 2
This graph can be translated. We can, for example, move the graph down 3 units and leave 5 units. The graph of f (x) = 2x+5 – 3 is as follows:
f (x) = 2x+5
This graph goes through the point and has a horizontal asymptote at y = -3. (- 5, – 2).
Graph 3
By multiplying the output by a constant, we may extend and shrink the graph vertically (see Stretches). f (x) = 32x, for example, is extended vertically by a factor of three:
f (x) = 32x
This graph goes through the point and features a horizontal asymptote at y = 0. (0, 3).
Exponential functions with various bases, such as f (x) = 3x and f (x) = 4x, can likewise be graphed. These graphs differ from the graph of f (x) = 2x by a horizontal stretch or shrink: multiplying the input of f (x) = 2x by 2 yields f (x) = 22x = (22)x = 4x.
As a result, the graph of f (x) = 4x is shortened horizontally by a factor of 2 when compared to f (x) = 2x:
f (x) = 4x
This graph goes through the point and features a horizontal asymptote at y = 0. (0, 1).
The graph of f (x) = axe does not necessarily differ by a reasonable factor from the graph of f (x) = 2x. As a result, it is useful to consider each basis separately, and to consider a different base as a horizontal stretch merely for comparative reasons.

An exponential function’s graph can also be mirrored across the x-axis or the y-axis and rotated about the origin, as shown in Heading.
An exponential function has the general form f (x) = cfax-h + k, where an is a positive constant and a1 and is the base. The graph goes through the point (h, c + k) and has a horizontal asymptote of y = k.
Horizontal Asymptote rules equation
We know that the vertical asymptote of the graph function y = f(x) with a straight line equation is x = an if at least one of the following requirements is met:
The limit of x is a – 0 f(x) = plus minus infinity.
Or
The limit of x is a + 0 f(x) = plus minus infinity.
Otherwise, at x=a, one of the one-sided limits must be equal to infinity.
For the straight-line equation, the limit of the oblique asymptote of the graph function y=f(x) is y=kx+b.
The picture of X tends to be plus infinity.
If and only if the two constraints listed below are satisfied.
f(x)/x = k is the limit of x that tends to plus infinity.
The limit of x is plus infinity [f(x) – kx] = b.
The straight line equation for the graph function y=f(x) is y=b, which is the asymptote of a function.
Assuming that the following limit is finite, X goes to plus infinity.
The limit of x tends to be plus infinity, hence f(x) = b.
The aforementioned limit applies to both x tends to infinity.
Example
Determine the asymptotes for the function f(x) = (3x – 2)/(x + 1)
Solution:
Given,
(3x – 2)/(x + 1) Equals f(x).
For x = -1, f(x) is not defined.
Find the one-sided bounds of the following function when x = -1.
Limit x tends to – a – 0 f(x) = limit x tends to minus 1 minus 0 3x – 2/ x + 1= -5/-0 = + infinity.
Limit x tends to – a + 0 f(x) = limit x tends to minus 1 plus 0 3x – 2/ x + 1= -5/0 = – infinity.
As a result, the function f(x) has a vertical asymptote at x = -1.
Let us now find the horizontal asymptotes by assuming that x goes to plus minus infinity.
Limit of x tends to infinity f(x) = limit of x tends to infinity 3x – 2/ x + 1 = Limit of x tends to infinity (3 – 2/x) / 1+1/x = 3/1 = 3
As a result, the function f(x) has a horizontal asymptote at y = 3.
K = limit of x tends to infinity f(x)/ x
= x’s limit approaches infinity 3x – 2/ x(x+1)
= x’s limit goes to infinity 3x-2/(x2 + x)
As a result, =0/1 = 0.
Similarly, we may get the same value for x – infinity.
Since k = 0, there are no oblique asymptotes for the given function.
Some frequently asked questions
What is the rule for horizontal asymptote?
- The function has no HA if the degree of the numerator is greater than the degree of the denominator.
- The function has one HA, which is y = 0, if the degree of the denominator is greater than the degree of the numerator.
- If the numerator’s degree equals the denominator’s degree, the function has one HA, which is y = the ratio of the leading coefficients in the numerator and denominator.
What are the rules for vertical asymptotes?
To discover the vertical asymptotes of a rational function, just set the denominator to zero and solve. Vertical asymptotes exist when the numerator is zero. Remember that dividing by zero is not an option. Because division by zero is not possible, the resulting graph avoids those regions.
How do you find the horizontal asymptote using limits?
If either limx→∞f(x)=L or limx→−∞f(x)=L a function f(x) will have the horizontal asymptote y=L. To discover horizontal asymptotes, we simply evaluate the function’s limit as it approaches infinity, and then again as it approaches negative infinity.
How do you identify vertical and horizontal asymptotes?
While vertical asymptotes explain a graph’s behaviour as the output becomes extremely big or very tiny, horizontal asymptotes help describe a graph’s behaviour when the input becomes very large or very small. Remember that the end behaviour of a polynomial will be the same as the leading term.
Which function has no horizontal asymptote?
If the degree of the numerator, P(x), is larger than the degree of the denominator, Q(x), the rational function f(x) = P(x) / Q(x) has no horizontal asymptotes (x).
How do you find the horizontal asymptote if there is no denominator?
The x-axis (y = 0) is the horizontal asymptote if the polynomial in the numerator has a lower degree than the denominator. There is no horizontal asymptote if the polynomial in the numerator has a greater degree than the denominator.
What is the horizontal asymptote?
The horizontal asymptote of a function y = f(x) is a line y = k when either lim x f(x) = k or lim x – f(x) = k. That is, it is a line that the graph (curve) of the function appears to approach as x or x -. It’s sometimes shortened as HA. In this scenario, k is a real number that the function approaches when x is either extremely large or extremely small. A horizontal asymptote for a function may or may not exist. However, the maximum number of asymptotes that a function may have is two. To put it another way, a function can have 0 asymptotes, 1 asymptotes, or 2 asymptotes.
Can you have a hole and a vertical asymptote?
When factors from the numerator and denominator cancel, a hole is formed. When a factor in the denominator does not cancel, a vertical asymptote is produced. A rational function’s scope is constrained by both holes and vertical asymptotes.
What are vertical isotopes?
A vertical asymptote is a vertical line that directs the function graph but is not a part of it. It can never be crossed by the graph since it happens at an x-value that is outside of the function’s scope. There may be more than one vertical asymptote for a function.