The Interval Notation Calculator is a completely free web utility. It does, however, display the number line for a set interval. In addition, the online interval notation calculator tool speeds up the computation. In addition, it shows the number line and inequality form in seconds. Furthermore, the Interval Notation Calculator determines the length of any interval between two numbers. The inequality is then represented using the topology that was chosen. Furthermore, interval notation provides a way to express real number line subsets. This calculator is the subject of this article.

Continue reading to learn more about it.
Interval Notation calculator definition
An interval in mathematics is the set of real numbers that lie between two integers. The three most prevalent methods for expressing intervals are as follows:
- Interval Notation Method
- Number Line Method
- Inequalities Method
In the interval notation approach, however, the beginning and ending integers will be represented by brackets. Then there are brackets, which come in two varieties: square brackets and round brackets. If the interval is wrapped in square brackets, the end values are included. Also, if the interval is enclosed in round brackets, the end values are not included.(7, 12) As an example, it specifies a range of numbers from 7 to 12, with 7 being omitted and 12 being included.
Read Also: Acid base reaction calculator: know about this calculator
We can describe Intervals using inequalities such as greater than, less than, more than or equal to, less than or equal to. Then, if a circle in a number line representation is full, it indicates that the final value is included. If a circle is an open circle, the final value is not included. Furthermore, Interval Notation Calculator is a free online tool that shows the given gap on a number line, expresses the inequality using the selected topology, and determines the length of the interval between two numbers. To use the interval notation calculator, enter the values in the input boxes.
Interval notation calculator with steps
Follow the steps below to obtain the length of the interval, its number line representation, and the inequality based on the given topology using the online interval notation calculator.
- Go to any interval notation calculator on the internet.
- Then, using the drop-down box, select a topology and enter the numbers into the corresponding input areas.
- Then, click the “Calculate” button to obtain the interval’s length, number line representation, and inequality.
- Finally, use the “Reset” button to clear the fields and enter new values.
Interval Notation Calculator from equation
Plot the number line interval [2, 4], and then determine the inequality, topology, and length. To double-check your results, use the online interval notation calculator.
Solution:
Inequality = 2 inequality x inequality 4
Closed Interval = Topology
Length = 4 minus 2 = 2
On a number line, draw the interval [-3, 1) and specify the inequality, topology, and length. To double-check your results, use the online interval notation calculator.
Solution:
Inequality = -3 inequality x less than 1
Left closed, right open is the topology.
Length = 1 minus (-3) = 4
Similarly, the interval notation calculator used to calculate the number line representation, inequalities, topologies, and length for the intervals shown below:
[-5, -2] (5, 9)
Interval Notation Calculator domain
In mathematics, a domain is the set of possible values “x” of a function that will result in the output value “y.” It is the sum of the potential values of independent variables. The range of a function is the set of outcome values of the dependent variable. This is the set of output values when the x values are replaced. It is similar in that the output is created when the input values are supplied to the function.
In summary, a domain is the set of values that the function f(x) allows, whereas a range is the set of values that the function does not accept. The domain represents the replacement set, whereas the range represents the solution set.
Example 1
f(x)=1/x^2 – 1
The only thing we have to be concerned about is the denominator being zero. As a result, we know that x squared minus one cannot equal zero. This indicates that x squared cannot be equal to one. Then, if we take the square root of both sides, x cannot be greater than or less than one. So, when we define our domain in interval notation, we will be able to move from infinite to infinity. We’ll also go all the way to the negative one.
(- infinity, – 1) union (-1, 1) union (1, infinity)
As a result, this is our domain.
Example 2
f(x)=2 by root over 3x+5
We also have a square root in this equation, but no negative radical. We understand that 3x + 5 cannot equal zero. It must be bigger than or equal to zero. It has to be uplifting. Also, because of the radical, it cannot be negative, and it cannot be zero because it is in a denominator. So, when we solve this for x, we see that three x must be bigger than negative five. Also, by dividing both sides by three, we get that x must be bigger than negative five-thirds. So, to represent the domain in interval notation, start at -0.33 and work your way up to infinity. A parenthesis always followed infinity. The only concern is whether we want to include the negative five-thirds, which we don’t.
(-5/3, infinity)
So that gets a parenthesis as well, and there we have our domain.
Interval Notation Calculator graph
If a function’s domain and range are both sets of real numbers, it is a real function. Many of the functions you’ve undoubtedly encountered before real functions with Domain = R. As an example, consider the function y=3x. The graph of this function shown in the sections below.
Line graphs are probably something you’ve seen before. Then you’re probably used to putting arrows at the end of phrases. Furthermore, this is done to demonstrate that the line may be drawn in both positive and negative directions in terms of domain and range forever. The preceding line, on the other hand, only shows the function y=3x on the interval [-3, 3].
The square brackets indicate that the graph comprises the endpoints of the intervals, x = -3 and x = 3. This has another name which is close interval. A closed interval’s ends are contained inside it. An open interval, on the other hand, has no beginning and no finish. Parentheses denoted an open interval parentheses.

For example, (-3, 3) represents the range of numbers between -3 and 3, omitting -3 and 3. You might have noticed that the open interval notation looks similar to the notation for a planar point (x, y). To avoid confusing a point with an interval, it is necessary to thoroughly analyse an example or a homework project! The context usually makes the distinction clear.
Example 1
You were presented with a dilemma earlier over the purchase of tacos for lunch.
You only have $15 to spend on lunch, and tacos are $1.25 each. Obviously, the total cost would be graphed as a function of the number of tacos ordered, but how would you specify that the graph not include amounts greater than $15 or less than $3.75 (one taco each)?
Set the domain interval to [3.75, 15] to specify that the cost of lunch graph only includes values between $3.75 and $15.00.
Example 2
Determine the following sets:
(−3,9]
The integer ranges between -3 and 9, omitting the precise value of -3 but including 9.
[−23,12]
The integer range from -23 to 12 “contains” the numbers -23 and 12.
(infinity,0) All numbers less than or equal to zero, excluding the number zero.
Example 3
To describe the specified intervals, use interval notation:
Every positive number (0,+ infinity)
Because there is no such thing as a positive or negative zero. Because there is no maximum positive number, we define infinity as the highest possible value and use the symbol “” to signify that it cannot be reached.
The digits -eight to -two hundred forty-two, inclusive. [-8,242].
Because both values are present, the “[” symbol used on both ends.
All negative, zero, and positive numbers ranging from one to nine (−∞,9].
The “(” implies that negative infinity is not possible, but the “]” shows that 9 is part of the set.
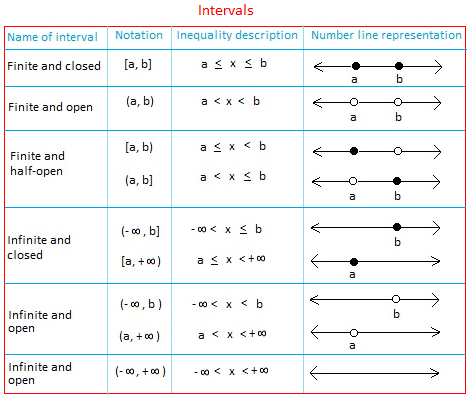
Interval notation calculator chart

| Interval notation | Inequality notation | Description |
| [a,b]
[a,b] |
A inequality x inequality b
A inequality inequality b |
The value of x is between a and b, including a and b, where a, b are real numbers. |
| (a,b)
(a,b) |
a less than x less than b
a less than x less than b |
The value of x is between a and b, not including a and b. |
| [a,b)
[a,b) |
A inequality x less than b
A inequality x less than b |
The value of x is between a and b, including a, but not including b. |
| (a,b]
(a,b] |
a less than x inequality b
a less than x inequality b |
The value of x is between a and b, including b, but not including a. |
| (a,∞)
(a,∞) |
x>a
x>a |
The value of x is strictly greater than a. |
| [a,∞)
[a,∞) |
x≥a
x≥a |
The value of x is greater than or equal to a |
| (−∞,a)
(−∞,a) |
x less than a
x less than a |
The value of x is strictly less than a |
| (−∞,a]
(−∞,a] |
X inequality a
X inequality a |
The value of x is less than or equal to a. |
Interval notation calculator inequality
The collection of real numbers that fall between any two given real numbers. Interval notation expresses it. Intervals represented inequalities. There are four types of intervals. If we have two endpoints, x and y, and x y, we may categorise the intervals as follows:
Open Interval
This does not include the two ends. If we have a number z that is between x and y, we may write the inequality as x z y. Round brackets represent an open interval, i.e. (x, y).
Closed interval
This range includes both ends. The inequality is represented as x z y. Square brackets are used to denote closed intervals, such as [x, y].
Right Interval Half-Closed
In this interval, just the left endpoint is included, while the right endpoint is excluded. The inequality is denoted by x z y. The interval’s left side is contained by a square bracket, while its right side is enclosed by a round bracket, i.e., [x, y].
Only the right endpoint is included in this interval, whereas the left is excluded. The inequality is x z y. The left side utilises a circular bracket, but the right side uses a square bracket, i.e. (x, y).
The following formula may be used to calculate the length of the distance between x and y:
Length equals y minus x.
Interval notation calculator union
A U B (sometimes spelled “A or B” or “A union B”) implies a set that includes all of the components of A and B. Use the union B formula to get the union of two sets A and B. The union is obtained by simply putting all of A and B’s components in one set and removing duplicates. In other words, A U B may be calculated without utilising the A union B formula.
Let’s say we have two sets, A and B. A U B is now built up of components picked one at a time from both sets A and B. (leaving duplicates). Our representations are as follows:
- n(A U B) = the total number of elements in A U B
- n(A) denotes the number of items in A.
- n(B) denotes the number of items in B.
- n(A ∩ B) = The number of elements that both A and B share.
The total number of items in A and B, including common elements, is given by the sum of n(A) and n(B). This indicates that the number of shared components is doubled.
To balance this and guarantee that all components are counted only once, we subtract n(A) from n(A) + n(B), yielding the formula for the number of elements in A U B:
n(A U B) = n(A) + n(B) – n(A ∩B)
Example 1
If A = 1, 2, 3, 4, and B = 2, 3, 6, 7, get A U B.
Given this, the solution is as follows:
A = 1, 2, 3, 4, 5
B = 2, 3, 6, 7, 8
Then, using the A union B formula, we can easily construct A U B by storing all of A and B’s components in a single set while eliminating duplicates.
As a result of this, A U B = 1, 2, 3, 4 1, 2, 3, 4, 6, 7 = 1, 2, 3, 4, 6, 7
The components of the solution set do not need to be in any specific order.
1, 2, 3, 4, 6, 7, 8 = A U B
Example 2
Determine the probability of randomly getting an ace or a black card from a deck of 52 playing cards.
Solution: We know that a deck of 52 playing cards has 26 red cards and 26 black cards, as well as four aces, two of which are red and two of which are black.
Assume A is receiving an ace and B is receiving a black card. The occurrence of obtaining a black ace card is thus denoted as A ∩ B.
P(A) = 4/52 = 1/13 P(A) = 4/52 = 1/13 P(A) = 4/
Then, P(B) = 26/52 = half
Then, P(A) = 2/52 = 1/26
As a consequence, the chance of obtaining an ace or a black card is P(A U B), or
P(A) + P(B) – P(A ∩ B)
=4/52 + 26/52 – 2/52
=28/52
=7/13
As a result, the needed probability is 7/13.
Interval notation calculator Math
To be elected President of the United States, a person must be at least 35 years old. Please provide an interval to represent this data.
Solution: Let’s utilise the letter A to represent the president’s age.
A should be at least 35 years old.
This means that A must be more than or equal to 35.
As a result, the disparity, A 35, exemplifies this.
As a result, the required range is [35, infinite].
A school’s participation in an Olympiad exam requires a minimum of ten pupils. Use interval notation to represent this.
Solution:
If x represents the number of pupils in a class, x should be larger than or equal to 10.
This translates to x ≥10
[10,infinity] is the interval notation.
As a result, [10,infinity] represents the number of pupils.
Lola needs at least 1500 calories per day, but her calorie intake should not surpass 1800. Using interval notation, represent the total number of calories she might consume.
Solution:
Let’s double the quantity of calories by x.
1500 inequality x inequality 1800 gives the inequality expressing the potential number of calories.
The interval notation [1500, 1800] denoted the inequality.
[1500, 1800] is the needed interval notation.
Some frequently asked questions
What is interval notation in math?
Interval notation is a method of expressing real number line subsets. A closed interval is one that contains its ends, for as the set {x | −3inequalityxinequality1}. We use closed brackets []: [3,1] to represent this interval in interval notation.
What is an interval example?
An interval scale has order, and the difference between two numbers is significant. Temperature (Farenheit), temperature (Celcius), pH, SAT score (200-800), and credit score are examples of interval variables (300-850).
What is Interval Notation Calculator?
However, the Interval Notation Calculator is a free online tool. However, it displays the number line for a given interval. Also, the online interval notation calculator tool accelerates the calculation. Also, it displays the number line and inequality form in seconds. Moreover, the Interval Notation Calculator computes the length of any interval between two integers. Then, it represents the inequality based on the topology chosen. Moreover, Interval notation is a method of expressing real number line subsets.
What does U mean in interval notation?
A U B (we can read it as “A or B” (or) “A union B”) denotes a set that contains all of the components of A and B. To get the union of two sets A and B, use the union B formula. Simply placing all of A and B’s elements in one set and deleting duplicates yields the union. In other words, It is possible to calculate A U B without using the A union B formula.
How do you do intervals on TI 84?
- Select the Z Interval.
- Scroll down to TESTS after pressing Stat.
- Enter the required information.
- The calculator will request the following data:
- Analyse the results.
- When you press ENTER, the population mean’s 95 percent confidence interval will be shown.
What is interval measurement?
An interval measure is one in which the distance between the characteristics, or answer alternatives, has a real meaning and is of equal length. Variations in the values indicate variations in the property. The difference between 3 and 4 is equivalent to the difference between 234 and 235.
What is the interval of data in the graph?
An interval is the space between each value on a bar graph’s scale. In other words, the interval is the relationship between the units you’re using and their graph representation, or the distance between markers. You select intervals depending on the data set’s value range.
What’s a 90 confidence interval?
You have a 10% probability of being mistaken with a 90% confidence interval. A 95% confidence interval would be wider than a 95% confidence interval (for example, plus or minus 4.5 percent instead of 3.5 percent).
What is an example of an Interval notation calculator?
f(x)=1/x^2 – 1
The only thing we really have to worry about is the denominator being zero. So, we know x squared minus one cannot equal zero. This means x squared cannot equal one. Then, if we take the square root of both sides, x cannot equal plus or minus one. So, when we go to write our domain in interval notation, we are going to be able to go from infinity. Also, we are gonna go all the way to the negative one.
(- infinity, – 1) union (-1, 1) union (1, infinity)
So, this is our domain.