The idea of energy, and its conservation, proved immensely beneficial in the study of mechanics. Therefore, we will study electrical interactions in the same way. Moving a charged particle in an electric field can cause the particle to gain or lose both kinetic and potential energy.
Lifting an item in a gravitational field takes effort and increases the potential energy of the object. Similarly, when two charged items are moved close to one other, a similar scenario happens. We already know that each thing is surrounded by an electric field that influences the additional charges. When the costs of two charged things are the same, they repel each other.
Moving these two items closer necessitates fighting the repulsive force, raising the system’s potential energy. However, moving two similar charges apart, on the other hand, reduces the potential energy. When the items attract each other, the situation is reversed: pulling them apart works against the force, increasing the system’s potential power, but bringing attractive charges closer together reduces the system’s potential energy. Depending on the scenario, it’s simple to see the shift in energy as a mountain or an inverted cone. We can also consider a positive point charge and the electric field that surrounds it.
If you want to know more about this topic, you’re welcome here. Read on as we explore all the facts about this.

Electric Field between Two Plates: Definition
Mathematically we define the electric field as:
E = F/Q
It is a vector. Moreover, it also has strength and direction. The direction is parallel to the force of a positive atom.
Characteristics of the Electric Field
- Every point in space has an electric field label linked to it. It specifies the magnitude and direction of the electric force experienced by a charge of +1 Coulomb at that location.
- The electric field may be readily measured by measuring the electric force on a small test charge at various places.
- It is defined as : E = Electric Force / Charge
- A positive charge causes the electric field lines to point away from it. Because an amount of +1 C would push it away. They are moving away from a positive charge and toward a negative charge. This is because a cost of +1 C would pull it in that direction.
- In a vector sense, the electric fields of many particles add together (component by component).
- We can also figure out electric field between two evenly charged plates. Thus, it is significantly more significant than the space between them.
Q
E = ———–
eps x A
Here,
Q is the charge magnitude on each plate.
Eps = free space permittivity.
Each plate’s area is denoted with the letter A.

Electric Field between Two Plates Formula
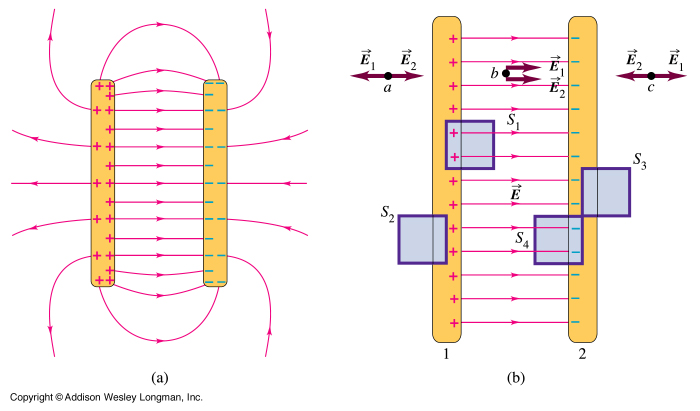
An electric field’s direction is definable as the direction in which a positive test charge would move. As a result, the electric field will be running from the positive plate to the negative plate. This sort of electric field is uniform and has a magnitude since the field lines are parallel. E = V/d, where V is the voltage supplying from the battery and d is the distance between the plates. We may use this info to determine it.
The electric field strength, E, can be quantified in one of two ways: in V/m or, equivalently, in N/C. To put it another way, describing the electric field strength as E = 10 V/m is comparable to expressing the electric field strength as 10 N/C.
V/d = (J/C)/m
[(nt m)/C]/m
nt/C
Because the field lines are parallel and the electric field between two similar plates is uniform, no matter where a test charge is in the area, it will feel the same force of attraction or repulsion. The equation F = qE determines the force, where F and E are vector variables, and q is a scalar number.
The distance between the plates in the diagram above is 0.14 meters. And the voltage between the plates is 28 volts. The UNIFORM electric field between the leaves would have a magnitude of
E = − ΔV/d
= − (-28 V) / (0.14 m)
= 200 V/m
The Electric Field between Two Plates of Capacitor
Static and dynamic charges, electric and magnetic fields, and their varied consequences are all studied in electromagnetism. Capacitors are devices that use an electric field to store electrical potential energy. As a result, the laws of electromagnetism apply to capacitors. This article will describe and explain some of the concepts that are necessary to comprehend capacitor operation. The electric field will be uniform in all points in space in this question.
Capacitors are electrical energy storage devices that are present in circuits. The energy sent to the capacitor is staying in an electric field produced between the capacitor’s plates. When a voltage is there across the leaves of a capacitor, a certain amount of charge accumulates. However, the stored energy is:
W= ½ CV^2
W stands for the stored energy, C for capacitance, and V for the voltage applied across the capacitor.

Electric Field between Two Plates between Different charge densities
The electric field will be perpendicular to the surface for an infinite sheet of charge. As a result, the electric flux will be generated exclusively at the ends of a cylindrical Gaussian surface. A cylindrical Gaussian surface perpendicular to the charge sheet is present in this situation. The resultant field is half that of a conductor at this surface charge density in equilibrium.
We may use Gauss’ law to determine the electric field between parallel conducting plates in opposite charges if they are considerable as infinite planes (neglecting to fringe). If the leaves are in equilibrium and there is no electric field inside the conductors. We may calculate the outcome of a charged conducting surface.
We can take three Gaussian surfaces using Gauss’ law. One has both plates, whereas the other two include each dish separately.
We have:
ESn + ESn = σ(a-b)/ε0 n
You should be able to demonstrate that an infinitely charged sheet generates a homogenous electric field oriented perpendicularly to the sheet using Gauss’s Law:
E= -(a-b)/2 n
This is on the left-hand side of the two plates
E= (a+b)/2 n
It’s in the center of the plates
Finally, E= (a-b)/2 n
We can write this on the right-hand side of the plates.
Electric Field between Two Plates with same charge densities
The electric field surrounding a point charge diminishes as the distance from the point increases, as we know from Coulomb’s law. However, by aligning two big, flat conducting plates parallel to each other, we can create a continuous electric field. Except at the plates’ edges, the area between the leaves will have a constant electric field if one of the plates is positive and the other stays negative.
Voltage is a unit of measurement for the electric potential difference between two locations (V). Because voltage is the change in potential difference, choosing a point to be the relative zero when measuring the voltage across a distance is essential.
The value of zero volts can be assigned to any location in a system, although it is most commonly the point of a point charge or one plate in a uniform electric field, as shown above. We may use a voltmeter to measure the voltage, also known as the electric potential difference.
V=Ed, the electric field intensity times the distance between the plates, is the electrical potential difference between the two plates. The final units in this statement are Joules/coulomb, which is Newtons/coulomb times metres. The quantity of potential energy per unit charge expresses itself as voltage. We may estimate the amount of effort required to move a charge against a field by multiplying the electricity.
W=Vq
The Magnitude of the Electric Field
An electric field’s amplitude and direction are also both vector variables. The method used to measure the strength of an electric field determines its magnitude. Assume that We may use the symbol Q to represent a charge of electricity. This electric charge produces an electric field; we’ll refer to it as the source charge because Q is the electric field’s source. We can use any extra order placed near the source charge to determine the strength of the source charge’s electric field. The charge we need to assess the electric field strength is a test charge since it is used to evaluate the field strength.
E = F/Q
The quantity of charge in the test charge is popular as the symbol q. When the test charge is in an electric field, it will feel an electric force that is either attractive or repulsive. This force will be represented by the letter F, as is customary. The force per charge in the test charge is magnitude of the electric field.
Its definition gives birth to the conventional metric units for electric field strength. The units of an electric field are force units divided by charge units since we call it force per charge. Newton/Coulomb or N/C are the conventional metric units in this situation.