The most frequent definition of a function’s domain, D, is the set of values for which we define it. A function f(x) constructed for real values x in R, for example, has domain R. We call it “a function over the reals.” The range refers to the collection of values that the function sends to D.
If we define a function on a set, we refer to that set as the domain. The range refers to the set of values that the function accepts. The function x², for example, converts reals (domain) to non-negative reals (range). The sine function converts real numbers (domain) to the closed interval [1,1]. (range).
One of the most effective approaches to study a function’s general behaviour is to determine its domain and range. The domain of a function, in simple terms, is the range of possible x values that can be fed into it, where x represents the independent variable. The range refers to the set of output values that are possible.
Because a negative number² provides a positive result, if the function is f(x) = x², the available input values (the domain) are all real numbers, and the output values are all positive real numbers. Although it isn’t normally essential to find the range of a function on a calculator, you can do so with ease using a graphing calculator.
You may check the range and domain of a function online for free using the Domain and Range Calculator. Our online domain sped up the procedure and range calculator, and it displayed the result in a fraction of a second.
Domain And Range Calculator
The operations of a vending (soda) machine can be related to mathematical functions. You can choose from a variety of sodas after depositing a particular amount of money. Similarly, we input distinct numbers into functions and get new numbers as a consequence. We define functions by their domain and range. We can purchase a drink using quarters or one-dollar bills. If you put in cents, the machine will not give you any soda flavour. As a result, the domain depicts the possible inputs, which are quarters and one-dollar bills.
Read Also: Completing the square calculator — a complete guide
You won’t receive a cheeseburger from a Pepsi machine, no matter how much you pay. As a result, the range refers to the various outputs that we can have here, namely the different flavours of soda in the machine. Let’s look at how to find the domain and range of a function, as well as how to graph them. The calculator will determine the domain and range of the single-variable function.
The domain calculator allows you to quickly find the domain of a simple or complicated function in both interval and set notation.
Domain And Range Calculator With Steps
The following is how to use the domain and range calculator:
Step 1: In the input field, type the function.
Then, step 2: To retrieve the output, click the “Calculate Domain and Range” button.
Then, step 3: In the new window, the domain and range will be presented.
What is Domain and Range?
We define domain in mathematics as the set of feasible “x” values for a function that will result in the output value “y.” It is the collection of independent variables’ potential values. The set of resulting values of the dependent variable is defined as the range of a function. When the x values are substituted, this is the set of output values. It’s similar in that the function will produce the output when the input values are given to it.
In simple terms, a domain is the set of values for which the function f(x) is defined, whereas a range is the set of values that the function accepts. The range is known as the solution set, and the domain is known as the replacement set.
Domain And Range Calculator Definition
A function’s domain is the set of input values, x, for which it is defined. In the image below, the domain is indicated in the left oval. For each member of the domain, the function returns an output value, f(x). The range of the function is the set of values that the function produces, and those values are depicted in the right hand oval in the image below. A function is a relationship that takes domain inputs and outputs values in the range. A function’s rule is that there is exactly one output for each input.
The set of ordered pairings in this mapping also indicates that it is a function because none of the x-values repeat: (1,1), (1,1), (7,49), (0.5,0.25); each input maps to exactly one output. Because the points do not form a vertical line, we can also tell that the set of ordered pairs is a function based on the graph of the ordered pairs. There would be two points on a graph of a vertical line if an x value repeated, which would not be a function.
It’s vital to remember that not all functions have a domain of real numbers. Because you can’t divide a number by zero, the function f(x)= 1x isn’t defined for x= 0. The domain of f in this example is the set of all real numbers except 0. x≠0, to be precise. As a result, this function’s domain is R0.
Domain and Range Calculator of a Function
A function’s domain and range are its two fundamental components. The domain of a function is the set of all its input values, whereas the range is the function’s possible output. Range is a domain function. A is the domain, and B is the co-domain, if there is a function f: A B that maps every element of A to elements in B. ‘b’ is the image of an element ‘a’ under a relation R, where (a,b) € R. The set of photos is the function’s range. In general, a function’s domain and range are denoted as follows: domain(f) = x € R, range(f)=f(x): x € domain(f).
Domain of a Function
A function’s domain refers to “all the values” that go into it. The domain of a function is the set of all the function’s possible inputs. Consider this box as a f(x) = 2x function. The domain is simply the set of natural numbers, and the output values are referred to as the range, when the values x = 1,2,3,4,… are entered. However, because f(x) = 2x is defined for all real values of x, its domain is the set of all real numbers indicated by (-∞,∞). The following are the general formulas for determining the domain of various sorts of functions. R is the set of all real numbers in this case.
R is the domain of any polynomial function (linear, quadratic, cubic, and so on).
The domain of a square root function x is x greater than or equal to 0.
R is the domain of an exponential function.
The domain of a logarithmic function is x times greater than zero.
Set the denominator to 0 to get the domain of a rational function y = f(x).
Range of a Function
The set of all a function’s outputs is its range. Example: Consider the function f: A→B, where f(x) = 2x and A and B each represent a set of natural integers. A is the domain, while B is the co-domain in this case. The range is then the output of this function.
The range is defined as a group of even natural numbers. The domain elements are referred to as pre-images, while the mapped elements of the co-domain are referred to as images. The set of all pictures of the domain’s elements (or) the set of all the function’s outputs is the range of the function f.
We’ll examine how to find the range of different sorts of functions in the next sections. The general formulas for determining the range of different types of functions are listed below. R is the set of all real numbers in this case.
R is the range of a linear function.
Range of a quadratic function y = a(x-h)2 + k is:
If an is more than 0, y is greater or equal to k, and if an is less than 0, y is less or equal to k.
A square root function’s range is y greater or equal to 0.
An exponential function’s range is y times 0.
R is the range of logarithmic functions.
Solve for x and set the denominator to 0 to obtain the range of a rational function y = f(x).
Domain And Range Calculator with Points
- Suppose X = {1, 2, 3, 4, 5}, f: X → Y, where R = {(x,y) : y = x+1}.
- Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
- Range = the output values of the function = {2, 3, 4, 5, 6} and the co-domain = Y = {2, 3, 4, 5, 6}
Let’s understand the domain and range of some special functions taking different types of functions into consideration.
Domain and Range Calculator of Exponential Functions
The function y = ax, a is greater than or equal to 0 is defined for all real numbers. As a result, the exponential function’s domain spans the entire real line. The exponential function yields a positive number every time. As a result, the exponential function’s range is of the form y= |ax+b| is y ∈ R , {y is greater than 0}. Domain = R, Range = (0, ∞)
Example: Look at the graph of this function f: 2x
domain and range of a function 2^x
Observe that the function’s value approaches 0 as x tends to, but it will never reach that value. The following are the domain and range of exponential functions:
The set R serves as the function’s domain.
Range: When using the exponential function, you’ll always get positive real values.
Domain and Range Calculator of Trigonometric Functions
Examine the graphs of the sine and cosine functions. It’s worth noting that the functions’ values swing between -1 and 1, and they’re defined for all real numbers.
As a result, for each sine and cosine function:
Domain: The set R is the domain of the functions.
The functions have a range of [-1, 1].
All trigonometric functions have the following domain and range:
Domain and Range Calculator Graph
We can also use graphs to determine the domain and range of functions. However, we call the set of possible inputs, the domain. We make up the domain of a graph with all the x-axis input data. On the y-axis, the range represents the set of possible output values.
Finding the range of a function is as simple as graphing it and looking for the y-values covered by the graph. It’s enough to check if a quadratic function has a maximum or minimum value to determine its range. The y-coordinate of a quadratic function’s vertex determines its maximum/minimum value.
Set the denominator to 0 and solve for the variable to find the domain of the rational function. We define the domain as all of the values along the x-axis from left to right, and we define the range as the graph’s span from top to bottom.
Domain and Range Calculator From Graph
If the graph of a function is given/known, finding its domain and range is fairly simple. The domain is the set of x values that we cover by the graph, and the range is the set of y values that we cover by the graph. However, in writing the domain and range from a graph, keep the following in mind.
Examine the graph to see if it passes the vertical line test. Otherwise, it’s not a function, and such curves don’t normally have domain and range defined.
If the graph has a hole, the coordinates of that hole should not be in the domain or range.
If there is a vertical asymptote, the corresponding value of x in the domain should not exist.
Now, if there is a horizontal asymptote, the matching x value in the range should not exist.
When we divide a graph into parts, we receive several sets/intervals in the domain and range, which we then group together using the “union” symbol ().
If there is an arrow at the end of a curve, it implies that the purpose of the curve’s design is to stretch in that direction indefinitely.
Here’s an example of a graph, and we’ll use it to determine the domain and range.
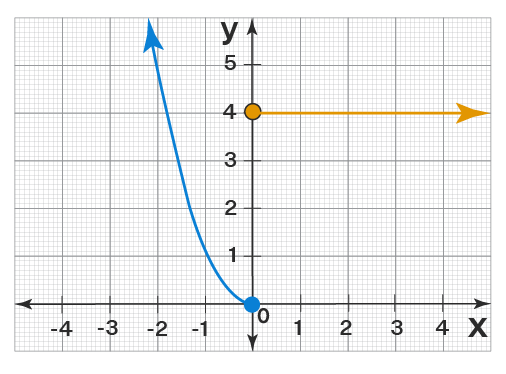
In the above graph:
- The graph encompasses all ∞-values from – to ∞. (because of arrows, the two curves extend infinitely in the given directions). As a result, the domain = (-∞, ∞).
- The graph encompasses all y-values greater than, equal to, or equal to 0. (see there is no part of the curve that is below the y-axis). As a result, the range is [0, ∞].
Domain and Range Calculator of an Absolute Value Function
For any real numbers, we define the function y=|ax+b|. As a result, the set of all real numbers is the domain of the absolute value function. When we calculate a number’s absolute value, it always yields a non-negative answer. An absolute value function of the form y= |ax+b| has a range of y € R | y is larger than or equal to 0. An absolute value function’s domain and range are as follows:
Range = [0,∞) Domain = R
Example: |6-x| Domain: The set R is the function’s domain.
The absolute value function always returns a non-negative value, as we already know. For any x, |6-x| is greater than or equal to 0.
Domain and Range Calculator of a Square Root Function
Only when x is higher than or equal to -b/a, we can write y=√(ax+b).
The set of all real integers bigger than or equal to b/a is the domain of the square root function. We know that taking the square root of something always yields a positive number. As a result, we define a square root function’s range as the set of all non-negative real numbers. A square root function’s domain and range are as follows:
Domain = [-b/a,∞), Range = [0,∞)
Example: y= 2- √(-3x+2)
When the value inside a square root function is a non-negative number, you can define the domain. As a result, -3x+2 is higher than or equal to 0 for a domain.
-3x exceeds or equals -2, while x is less than or equal to 23.
The square root function produces a non-negative value, as we already know.
√(-3x+2) is greater than or equal to 0.
Multiply -1 on both sides.
-√(-3x+2) is less than or equals to 0.
Adding 2 on both sides.
2-√(-3x+2) is less than or equals to 2.
y is less than or equals to 2.
Domain And Range Calculator with Solution
Find the domain and range of the function (x+1)/(3-x).
Solution:
At first, we will set the denominator equal to 0, and then we will solve for x.
3 – x= 0
– x = – 3 ⇒ x = 3
As a result, 3 will be removed from the domain.
As a result, the domain is the set of real numbers x, where (x is less than 3) and (x is more than 3). (x is greater than 3 )
Let’s look at the y=(x+1)/ range (3-x)
Let’s see if we can solve the given problem for x.
(3 – x)y = x + 1
3y – xy = x + 1
3y-1 = x + xy
x(1 + y) = 3y – 1
x = (3y – 1)/(1 + y)
The final equation is a fraction and we cannot define a fraction when its denominator is zero.
So 1+y ≠ 0 ⇒ y≠ -1
Therefore, the range of the given function is the set of all real numbers excluding -1
Domain = (-∞,3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞)
Answer: The domain and range of the function(x+1)/(3-x) = Domain = (-∞,3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞).
FAQs on Domain and Range Calculator
What is the Domain and Range of a Function?
A function’s domain and range are the set of all the inputs and outputs it can produce, respectively. The domain and range of a function are crucial considerations. The domain represents all of the potential input values from the set of real numbers, while the range represents all of the function’s output values.
How Do You Write the Domain and Range?
We define the domain and range of a function as the set of all possible inputs and outputs for the function, respectively. One can write the domain and range in ascending order from the smallest to the largest values. You can write the range from the top of the graph to the bottom, and the domain from left to right.
What is The Natural Domain and Range of a Function?
The natural domain and range of a function are all of the function’s conceivable input and output values, respectively. Domain(f) = {x∈R} and range(f)={f(x):x ∈ domain(f)}.
What is The Domain and Range of a Constant Function?
Let f(x)=k be the constant function. R, or the set of real numbers, determines the scope of a constant function. The singleton set, k, determines the range of a constant function. We express constant function’s domain and range as domain = x€R and range = k, which is a singleton set.
How to Find the Domain of a Function which is Rational?
We simply set the denominator not equal to zero to find the domain of a rational function. To find the domain of f(x) = 2/(x-3), for example, we set x-3 0 and solve for x3. As a result, we define the domain as the set of all rational integers excluding 3. In interval notation, we can represent this as (-∞, 3) U (3, ∞).
How to Find the Range of a Rational Function?
To find the range of a rational function, we just solve the equation for x and apply set the denominator not equal to zero. For example, to find the range of y=2/(x-3), solve it for x first. Then we get, x-3 = 2/y and from this, x = (2/y) + 3. Then its range is y≠0 (or) in interval notation, (-∞, 0) U (0, ∞).
What are the Rules to Find the Domain of a Function?
Here are some general guidelines for determining the domain of various sorts of functions:
The domain of f(x) = polynomial is the set of all real numbers.
The domain of f(x) = 1/x is the set of all real numbers except x≠0.
We define the set as f(x) = x, if the set of all real numbers such that x is higher than or equal to 0. We define the domain as f(x) = x.
The domain of f(x) = ln x is the set of all real numbers when x is bigger than 0.
How to Find The Domain and Range of Function Algebraically?
Let the function be y = f(x). Let’s use algebra to determine the domain and range of this function.
To determine the values of the independent variable x, we simply solve the equation to determine the domain of the function. To get the function’s range, just write x = g(y) and then discover the domain of g(y).