When the numerator polynomial has a higher degree than the denominator polynomial, oblique asymptote or slant asymptote occurs. As x approaches infinity or minus infinity, the function approaches a slanted line. There can be no more than two oblique asymptotes in a function, and certain functions will have no oblique asymptotes at all. Enter the rational equation into our online Slant Asymptote or Oblique Asymptote calculator to discover the slant asymptotes values.
Oblique asymptotes arise when the degree of the numerator is one higher than the degree of the denominator for rational functions. Long division can be used to find the oblique asymptote equation in this example. To make oblique asymptote calculations easier, use our Slant asymptote calculator. The Slant Asymptote Calculator is a free online tool that displays the function’s asymptote value. The computation is faster using our online slant asymptote calculator, which displays the asymptote value in a fraction of a second.
What is Slant Asymptote Calculator
When the degree of the numerator polynomial is greater than the degree of the denominator polynomial, a slant asymptote, also known as an oblique asymptote, arises in mathematics. The slant asymptote produces a linear function that is not parallel to either the x-axis or the y-axis. The oblique asymptote is simple to compute. It can be calculated by dividing the numerator polynomial by the denominator polynomial using either the synthetic or long division methods. The term “asymptote” refers to a line that is approached by a curve but does not meet it. As the curve approaches infinity, it joins the line.
Slant Asymptote Calculator with steps
The following is how to use the slant asymptote calculator:
Step 1: In the input field, type the function.
Then, step 2: To get the result, click the “Calculate Slant Asymptote” button.
Then, step 3: In the next window, the asymptotic value and graph will be displayed.
You can reset the game as many times as you wish. The first result shown is horizontal asymptote, but you can also see vertical and oblique asymptotes by clicking “Show Steps” next to the graph.
Let’s look at how you define asymptotes, the many forms of asymptotes, and some other relevant issues.
Types of Slant Asymptote Calculator
The value of the curve approaches infinity, the line approaches some value in horizontal asymptotes (both positive and negative). limx→±∞ f(x) = L
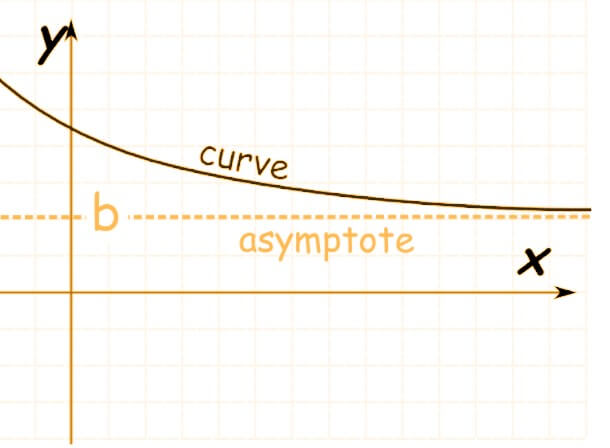
When the line approaches infinity as the function approaches a constant value, vertical asymptote occurs. limx→l f(x) = ∞
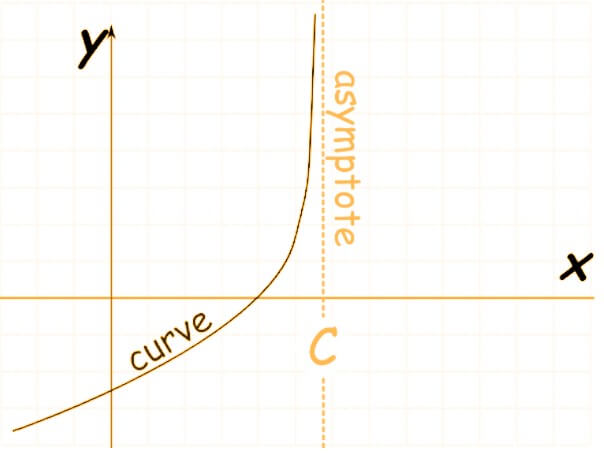
When a curved line approaches a linear function with a defined slope, it is called a Slant asymptote.
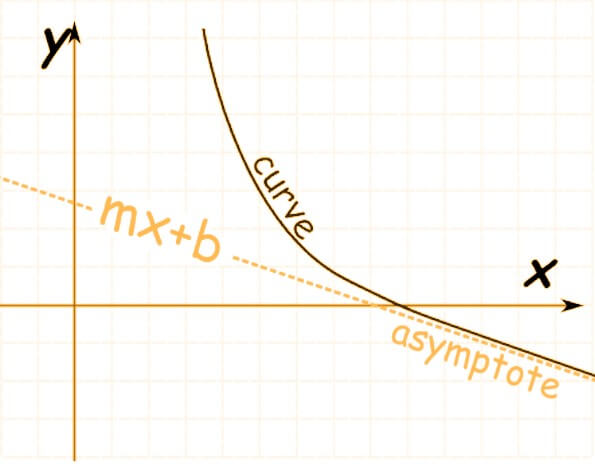
How to find Slant Asymptote Calculator
Any straight line that a graph approaches but never touches is an asymptote of a polynomial. It might be vertical, horizontal, or a slant asymptote, which is an asymptote with a slope. When the degree of the numerator is greater than the degree of the denominator, the polynomial has a slant asymptote.
Let’s look at how to locate the Slant Asymptote:
Step 1:
Check your polynomial’s numerator and denominator. Ensure that the numerator’s degree (that is, the highest exponent in the numerator) is greater than the denominator’s degree. A slant asymptote exists and can be found if this is the case.
Consider the polynomial x² + 5x + 2 / x + 3 as an example. Because the numerator has a power of 2 (x2) but the denominator only has a power of 1, the numerator has a higher degree than the denominator. As a result, the slant asymptote can be found. This polynomial’s graph is depicted in the diagram.
Step 2:
Make a long division issue for yourself. Place the denominator (the divisor) on the outside and the numerator (the dividend) inside the division box.
Set up a long division issue with x² + 5x + 2 as the dividend and x + 3 as the divisor for the example above.
X + 3 | X² + 5X + 2
Step 3:
Look for the first factor. Look for a factor that, when multiplied by the denominator’s highest degree term, produces the same term as the dividend’s highest degree term. Above the division box, write that factor.
In the preceding example, you would seek a factor that, when multiplied by x, yields the same term as the highest degree of x². That’s x in this example. Above the dividing box, write an x.
Step 4:
Find the factor’s product and the divisor’s total. To get your product, multiply it by a factor of two and write it beneath the dividend.
The product of x and x + 3 in the example above is x² + 3x. As demonstrated, write it under the dividend.
Step 5:
Subtract the lower expression from the upper expression by placing it under the division box. Underneath the line, write the result of your subtraction.
Subtract x² + 3x from x² + 5x + 2 in the previous example. As indicated, draw a line and write the answer, 2x + 2, beneath it.
Step 6:
Continue to divide. Rep these processes with your new dividend being the result of your subtraction problem.
In the example above, multiplying 2 by the divisor’s highest term (x) yields the highest degree term of the dividend, which is now 2x + 2. Add the 2 to the first factor and write x + 2 on top of the division box. Underneath the dividend, write the product of the factor and the divisor, and subtract again, as illustrated.
Step 7:
When you have a line equation, come to a halt. Long division does not have to be completed all the way to the finish. Continue until you have a line equation in the form axe + b, where a and b can be any values.
You can now stop in the previous example. Your line’s equation is x + 2.
Step 8:
Draw a line parallel to the polynomial’s graph. Verify that your line is an asymptote by graphing it.
In the previous example, you would need to graph x + 2 to demonstrate that the line runs alongside but never touches the graph of your polynomial, as seen below. As a result, x + 2 is a slant asymptote of your polynomial.
Slant Asymptote Calculator Definition
There are two possibilities: it exists or it does not. It can also be discovered by comparing the numerator and the denominator.
Read Also: Associative Learning: Definition, Theory & Examples
Slant asymptotes occur when the expression is incorrect and the numerator is one degree more than the denominator.
Polynomial long division will be required to determine its value. Ignore what’s left in the end. If we calculate the asymptotic value of (x2 + 3x + 2) / (x – 2), we get (x + 5) with a leftover of 12.
As a result, the linear equation that the curve approaches is y = x + 5.
Case – 2:
There can be no horizontal or oblique asymptote when the numerator is more than one degree bigger than the denominator.
Vertical Asymptote: Vertical asymptotes are drawn at the roots of the bottom function, where the value of the bottom function is zero. It can coexist with asymptotes that are horizontal or slant. However, it is critical that the expression be written in its simplest form.
Because a polynomial expression can have one, two, or more roots, a function can have more than one vertical asymptote. They can come in a variety of sizes.
Fun fact: y = Tan(x) has infinite asymptotes.
For example: f(x) = (2x – 7) / (x2 – 5x – 36)
To find the vertical asymptotic value, take the bottom value and factorize it.
x2 – 9x + 4x – 36 = 0
x(x – 9) + 4 (x – 9) = 0
(x + 4)(x – 9) = 0
However, the roots are x = -4 and x = 9. These are the two points where vertical asymptotes occur.
Slant Asymptote Calculator Graph
What is the best way to graph oblique asymptotes?
Graph the linear function as a slant dashed line once we know the equation for the oblique asymptote.
Meanwhile, make sure you brush up on your linear function graphing skills. But don’t panic; here are some helpful hints for graphing linear functions:
- Remember that the graph passes the -intercept, when the equation is of the type.
- Find a different point that solves the equation – usually the -intercept.
- The oblique asymptote is graphed by connecting these two spots with a dashed line.
To graph the oblique asymptote of f(x) =( x² – 6x + 9) / (x – 1), we use the intercepts of its quotient, x – 5.
| X intercept | 0 = x – 5
x = 5 Xint = ( 5, 0) |
| Y intercept | 0 – 5 = – 5
Yint = ( 0, -5) |
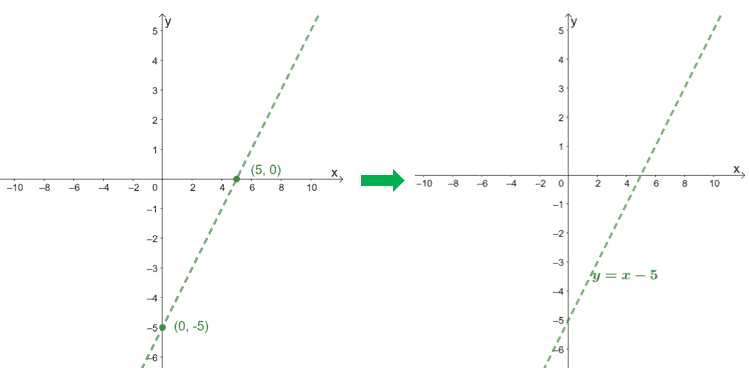
We can observe that f(x) has a vertical asymptote at x = 1 by looking at the denominator. Include the graph of f(x) as well to observe how the curve behaves.
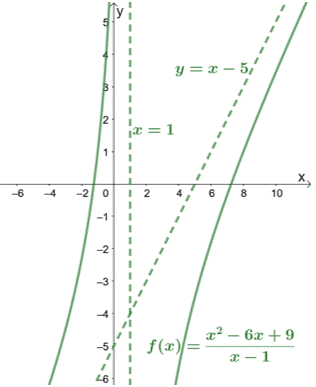
The asymptotes can also help us figure out how far the curves cover, as seen in the graph.
However, we can quickly see that the function’s numerator is one degree higher than its denominator by looking at the graph for oblique asymptotes.
Slant Asymptote Calculator Properties
We’ve already learnt a lot about oblique asymptotes, so let’s review the most significant properties before moving on to more instances.
The function has an oblique asymptote if the numerator is exactly one degree higher than the denominator.
We expect the oblique asymptote to return a linear function because its general form is y= mx + c.
However, graph the linear function using the intercepts of the oblique asymptote as guides.
Also, don’t forget to brush up on the previous topics we discussed in this article. Try out the sample problems we’ve supplied when you’re ready!
Slant Asymptote Calculator Example
Slant Asymptote Calculator Example 1
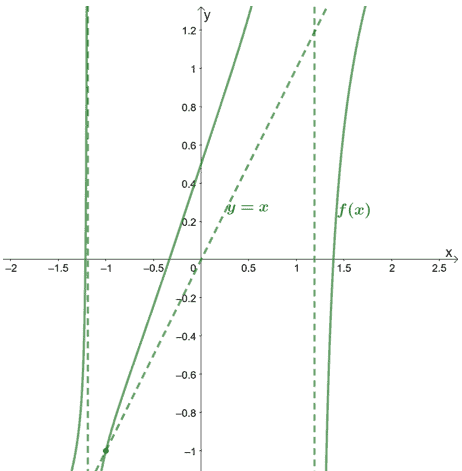
Given that when the numerator is divided by the denominator of f(x)= (x^5 + 5x – 10x + 2x – 1) / (x^4 – 2), f(x) can be written as f(x) = x +{( – x – 1) /( x² – 2)}
- What is the oblique asymptote of f(x)
- Will f(x) have any other asymptotes?
- Where would the oblique asymptote and f(x) intersect?
Solution
However, recall that oblique asymptotes are of the form, y = mx + b, and can be determined by finding the quotient of f(x).
We have f(x) = x +{ (- x – 1 )/ (x^4 – 2)} so the oblique asymptote of f(x) is y = x.
f(x) has no horizontal asymptotes when a function has an oblique asymptote. However, we may equate the denominator to 0 and solve for x to discover the vertical asymptote.
x⁴ – 2 = 0
x⁴ = 2
X = ± ⁴√2
This means that f(x) has two vertical asymptotes at x = -⁴√2 and x = ⁴√2, in addition to the oblique asymptote.
We can equate y = x with y = x + (-x -1) / (x⁴ – 2) to locate the intersection point shared by the oblique asymptote and the function, then solve for x.
x + {( -x -1) / (x⁴ – 2)} = x
Or, x + {( -x -1) / (x⁴ – 2)} – x = x – x
Or, {( -x -1) / (x⁴ – 2)} = 0
-x – 1 = 0
x = -1
The intersection’s x-coordinate is -1, as can be seen. Substitute x = -1 into the oblique asymptote’s equation: y = -1 to get the y coordinate.
This signifies that f(x) and its oblique asymptote cross at the same point (-1,-1).
Let’s have a look at how the graph and its asymptotes would appear.
Slant Asymptote Calculator Example 2
Find the oblique asymptotes of the following functions.
- f(x) = x²- 25 / x – 5
- g(x) = x² – 2x + 1/ x + 5
- h(x) = ( x⁴ – 3x³ + 4x² + 3x – 2)/ (x² – 3x +2)
Solution
Always remember that we can identify oblique asymptotes by dividing the numerator and denominator of the function.
Using the difference of two squares as a starting point,
a² – b² = (a – b)(a + b), x² – 25 can be factored as
(x – 5)(x + 5).
As a result, f(x) can be reduced to (x + 5).
- This means that at y= x+5, f(x) has an oblique asymptote.
Because the divisor is a binomial, synthetic division is the best option for the second expression.
1 – 2 1
-5 35
__________
1 -7 36
This means that g(x)= x – 7+ (36/ x – 5) so the quotient is x – 7.
- As a result, y=x-7 is the oblique asymptote of g(x). Because the denominator of the third function is a trinomial, we can use long division to get the quotient of x⁴- 3x³ + 4x² + 3x – 2 and x²-3x+2.
We can see that h() has a quotient of a² +2 from this. Because y =x²+2 is a quadratic asymptote, it will not form a line (a requirement for oblique or slant asymptotes). c. This indicates that h(z) does not have an oblique asymptote.
Slant Asymptote Calculator Example 3
An oblique asymptote of the function f(x) = p(x)/ q(x) runs through the positions (0, 10) and (5,0).
- What is the oblique asymptote equation for f(x)?
- What is p(x) and g(x) ?
Solution
Oblique asymptotes have the general form y = mx + b, where b is the y-intercept. Because f(x) passes through (0, 10), our oblique asymptote has the equation y = mx + 10.
Using the formula, find the m or slope of the line.
M = ( y2 – y1 )/ ( x2 – x1 )
M= 0 – 10 / 5 – 0
= -2
Hence, the equation of the oblique asymptote is y= -2x + 10.
Remember that the quotient of p(x) / q(x) returns the equation for the oblique asymptote of the function.
This suggests that p(x) and q(x) have a quotient of -2x + 10.
Frequently Asked Questions about Slant Asymptote Calculator
How do you find slant asymptotes?
Divide the numerator by the denominator to find the oblique or slant asymptote. Because the degree of the numerator is 1 more than the degree of the denominator, a slant asymptote exists. A slant asymptote is the equation y=mx+c.
Can a slant asymptote be a horizontal asymptote?
A graph can have both a vertical and a slant asymptote, but not both at the same time. A dashed horizontal (left and right) line is drawn through y = mx + b to create a slant asymptote on the graph.
How do you know if a graph crosses a slant asymptote?
Set the rational function equal to mx+b and solve for fx if there is a slant asymptote, y=mx+b. The line crosses the slant asymptote if f(x) is a real value. Meanwhile, substitute this value into the equation f(y) = mx + b and solve for f(y). The point at which the rational function crosses the slant asymptote will be determined as a result of this.
Are oblique and slant asymptotes the same thing?
Vertical asymptotes occur when the denominator of a rational function equals zero. An asymptote along a line is called an oblique or slant asymptote. When the degree of the denominator of a rational function is one less than the degree of the numerator, oblique asymptotes occur.
How do you find the slant asymptote?
Divide the numerator by the denominator to find the oblique or slant asymptote. Because the degree of the numerator is 1 more than the degree of the denominator, a slant asymptote exists. Any straight line that a graph approaches but never touches is an asymptote of a polynomial. It might be vertical, horizontal, or a slant asymptote, which is an asymptote with a slope. When the degree of the numerator is greater than the degree of the denominator, the polynomial has a slant asymptote.
Is a slant asymptote a horizontal asymptote?
A slant asymptote, like a horizontal asymptote, leads the graph of a function only when x is close to but not a vertical or horizontal line. If the degree of a numerator polynomial is 1 higher than the degree of the denominator polynomial, a rational function has a slant asymptote.
Is oblique and slant asymptotes the same thing?
An asymptote along the line y = mx + b, where m 0 is an oblique or slant asymptote. When the degree of the denominator of a rational function is one less than the degree of the numerator, oblique asymptotes occur.
How do you find slant asymptotes using limits?
Slant Asymptotes If limx→∞[f(x) − (ax + b)] = 0 or limx→−∞[f(x) − (ax + b)] = 0, then the line y = ax + b is a slant asymptote to the graph y = f(x). If limx→∞ f(x) − (ax + b) = 0, this means that the graph of f(x) approaches the graph of the line y = ax + b as x approaches ∞.
How do you know if a graph crosses a slant asymptote?
Set the rational function to mx+b and solve for x if there is a slant asymptote, y=mx+b. The line passes the slant asymptote if x is a real value. Solve for y by substituting this number into y=mx+b. The point at which the rational function crosses the slant asymptote will be determined as a result of this.
How do you know if you have an oblique asymptote?
Only when the numerator of f(x) has a degree one higher than the denominator do oblique asymptotes appear. Simply divide the numerator by the denominator using polynomial long division or synthetic division if you find yourself in this circumstance. The oblique asymptote will be the quotient (set to y).
What does an oblique asymptote look like?
Slanted asymptotes are another name for oblique asymptotes. That’s because its slanted form, y = mx + b, represents a linear function graph. Only when the numerator’s degree is exactly one degree greater than the denominator’s degree can a rational function have an oblique asymptote.
How do you find the slant height?
The formula a² + b² = c² can be used to compute the slant height. However, the altitude is a, the distance from the centre of the base to the point where the slant height segment begins is b, and the slant height is c in the formula.
What is a slant or oblique asymptote?
An asymptote along a line is called an oblique or slant asymptote. When the degree of the denominator of a rational function is one less than the degree of the numerator, oblique asymptotes occur. The function, for example, has a vertical asymptote at the line and an oblique asymptote around the line.




