Derivatives make for an extremely fundamental tool of calculus, without which mathematics cannot be imagined now. Derivatives of a function basically measure the change that the function will show given a change in its argument. When plotted, the derivative of a function at a particular point is the slope of the tangent to the point where the derivative is being measured.
Notations used in derivatives
There are more than one notations developed for the use in derivatives, each given by one of its pioneers.
The most common is the one by Gottfried Wilhelm Leibniz in 1675: dx, dy, and dy/dx. For higher derivatives, the symbol is dny/dxn, where n stands for the number of the order of which the derivative is. dnx/dyn represents the nth derivative of y with respect to x.
Joseph-Louis Lagrange further suggested a notation which we know as the prime notation. The notation uses a prime mark. Following this, the first derivative of a function, say f, is represented by f’. The second is shown as (f’)‘ = f”, and this goes on so. Many authors use romal numerals or even the number in parentheses in place of the prime mark to show the order of the derivative, like fiii or f(3) to show that the derivative in question is the third derivative of the function f.
Newton suggested the notation have a dot placed over the function to represent its time derivative, like ẏ. This is for the first derivative of y, our function. For the second derivative, one has to put two dots on top of the function.
The last major suggestion is Euler’s notation. It uses a differential operator D. When we apply D to the function f, we get Df, the first derivative of f. Dnf shows the nth derivative of f under this notation.
Derivative of ln x
A major part of derivatives is to memorise the basic derivative formulae. Another equally important aspect is to remember various rules which one must apply in order to differentiate a given function. The rules are uv rule or product rule, the u/v rule, the power rule, and the chain rule. The product rule is applied to those functions which are a product of two differentiable functions. Similarly, u/v rule is for functions which are a ratio of two differentiable functions. The power rule works when we are trying to differentiate a function which is raised to the power of some order. Lastly, the chain rule helps us to differentiate composite functions. Composite functions are essentially functions written inside another function, like sinx², where x² is a function written as a function of sine.Read Also:Completing the square calculator — a complete guide
All differentiable functions are differentiated using these rules, which are used in either combinations or individually as per the functions’ requirements.
The derivative of ln x is generally taken as given as a formula, that is, 1/x. But this entails a proof that the derivative of ln x is 1/x.
Derivative of ln x by first principle
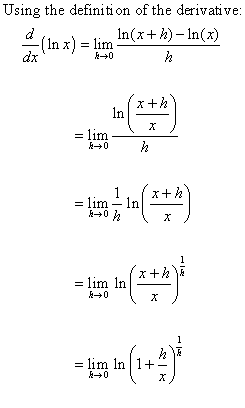
To differentiate ln x using first principle, let us start by assuming
f(x) = ln x.
By first principle, the derivative of f(x), that is f’(x), is given by the limit
f’(x) = lim h→₀ [f(x + h) – f(x)] / h.
And, since we took f(x) as ln x, we have
f(x + h) = ln (x + h).
Using these we get the expression
f’(x) = limh→₀ [ln (x + h) – ln (x)] / h.
Now, a logarithmic rule says that ln x – ln y = ln x/y. Applying the same here, we get
f’(x) = limh→₀ [ln ((x + h)/x)] / h
=> f’(x) = limh→₀ [ln (1 + (h/x))] / h.
Let us assume that h/x = t. This also gives us h = tx which we will use later. Following this assumption, we get,
f’(x) = limt→₀ [ln (1 + t)] / tx
=> f’(x) = limt→₀ (1/tx)[ln (1 + t)].
By virtue of another logarithmic property, which says y ln x = ln xy, we can write this expression as
f’(x) = limt→₀ ln (1 + t)(1/tx) = limt→₀ ln ((1 + t)1/t)1/x.
Now, since x is irrespective of the limit’s variable, we can write it outside of the limit like
f’(x) = (1/x) limt→₀ ln [(1 + t)1/t].
A limit formula is
Limt→₀ [(1 + t)1/t] = e. We use this to write the last expression as
f’(x) = (1/x) ln e
=> f’(x) = 1/x.
Since, ln e = 1.
So, this is how we find the derivative of ln x using first principle.
Derivative of ln x by implicit differentiation
Implicit differentiation is the differentiation of two sides of an equation with two variables by treating one of the variables as the function of the other variable. Implicit differentiation calls for the application of chain rule.
This method of finding out the derivative of ln x is relatively simpler compared to the first principle method. First of all, let us assume ln x = y. Therefore,
ln x = y
=> x = ey.
Now, let us differentiate both the sides of the equation above. Doing so gives us
1 = dy/dx ey
=> dy/dx = 1/ey
But, we have x = ey, therefore,
dy/dx = 1/x.
And, that we also took ln x = y means,
d (ln x)/dx = 1/x.
So, this is how we can find the derivative of ln x using implicit differentiation.
Derivative of ln x²

Derivative of ln x² is not difficult to find out. Having understood how to derive the derivative of ln x, it is not much different for ln x². One may choose to simply use the direct formula for the derivative of ln x to differentiate ln x².
The process requires the application of chain rule. The process is as follows:
d/dx (ln x²)
= 1/x² (d/dx (x²))
= 1/x² (2x)
= 2x/x²
= 2/x.
What we do here is easy to understand. First differentiate the logarithmic function which gives us 1/x², like the derivative of ln x is 1/x. Then we differentiate the function inside the logarithmic function, that is, x². Differentiating that generates 2x. We then multiply the two derivatives with each other and obtain the derivative of the total expression ln x².
The same logic is followed while differentiating ln x. It is just that since the derivative of x is 1 itself which when multiplied with 1/x gives 1/x itself, we do not generally show the process this way.
Therefore, we have just derived the derivative of ln x² as 2/x.
Derivative of ln x/x
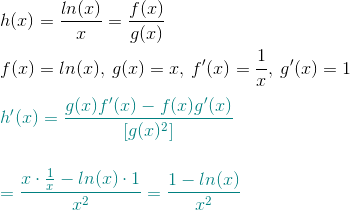
(ln x)/x is a seemingly complex function because the natural log function of x is divided by x itself. But it is easy to differentiate it. This question needs you to apply the u/v rule, that is, the rule for differentiating a function which is a ratio of two differentiable functions.
The u/v rule says the derivative of u/v is (u’v – v’u)/v², where u’ is the derivative of u, and v’ is the derivative of v.
Let us apply the rule to find the derivative of (ln x)/x. Follow the procedure below:
d/dx (ln x)/x
= {x(d/dx (ln x)) – (ln x)(d/dx (x))}/x²
= (x(1/x) – ln x)/x ²
= (1 – ln x)/x²
= 1/x – (ln x)/x².
The steps are easy to understand. We first multiply the derivative of the numerator, ln x in this case, with the denominator, x in this case, and from it subtract the derivative of the denominator multiplied with the numerator. Then we divide the whole expression by the denominator squared. Then the expression is simplified or brought to a required form which completes the process of differentiation.
So, this is how we find the derivative of (ln x)/x. The answer is 1/x – (ln x)/x².
Derivative of ln xy
Differentiating a function like ln xy is not much different from differentiating the natural logarithm of x, it is just that there is an additional coefficient of x which is a constant. Let us solve for the derivative of ln xy.
d/dx (ln xy)
= 1/xy (d/dx (xy))
= 1/xy (y)
= 1/x.
The procedure is extremely simple. This requires the application of chain rule. To differentiate this function, first differentiate the logarithmic function, bringing 1/xy out. Then differentiate the function xy. Here, y is a constant with respect to x, so the differentiation of xy with respect to x yields y. Then multiply the two derivatives, that is, 1/xy and y. The product will be 1/x, cancelling the y out from the numerator and the denominator. We find that the derivative of ln xy is the same as the derivative of ln x.
So, the derivative of ln xy is 1/x.
Derivative of ln(x²+1)
To find out the derivative of ln (x² + 1), one has to apply the chain rule. Differentiate the natural logarithmic function and then differentiate the function inside the natural logarithm. Let us start solving for the derivative of ln (x² + 1):
d/dx (ln (x² + 1))
= 1/(x² + 1) d/dx (x² + 1)
= (2x)(1/(x² + 1))
= 2x/(x² + 1).
For the derivative of the function ln (x² + 1), we first differentiate the natural logarithm and get 1/(x² + 1). Then we differentiate (x² + 1) and get 2x. Following the procedure of chain rule, we multiply both of these and get 2x/(x² + 1).
Therefore, the derivative of (ln (x² + 1)) is 2x/(x² + 1).
Derivative of ln (1/x)
Derivative of ln (1/x) needs the use of the chain rule of differentiation. Differentiating ln (1/x) is extremely easy; we just differentiate two very common expressions and then multiply them. Let us see how we go about the process:
d/dx (ln 1/x)
= (1/(1/x)) (d/dx (1/x))
= x (-(1/x²))
= –x/x²
= -1/x.
First of all, differentiate the logarithmic function. This will give x, which is the reciprocal of 1/x. Then differentiate the function inside the logarithmic function, 1/x. This is a common differentiation and yields -1/x². Then, multiply these two. Following this we get -1/x, cancelling the x in the numerator and one of the two xs in the denominator.
Therefore, the derivative of ln (1/x) is -1/x.
Derivative of ln xx
Finding the derivative of ln xx is a little tricky in terms of figuring out the process, but otherwise it is a very simple and intuitive sum. We do the differentiation in two parts: first differentiate the inner part and then the outer function of natural logarithm.
First, assume y = xx.
Therefore,
y = xx
=> ln y = ln xx
=> ln y = x ln x.
Now, differentiate both sides of the equation with respect to x.
d/dx (ln y) = d/dx (x ln x)
=> (1/y) dy/dx = (ln x) + 1
=> dy/dx = y((ln x) + 1)
=> dy/dx = xx ((ln x) + 1)
=> dxx/dx = xx ((ln x) + 1).
This is how we can find out the derivative of the inner function xx. What we do here is we first make the assumption that xx is equal to some arbitrary variable y. Then take the natural logarithm on both sides to get on the right hand side the expression ln xx. After this, we differentiate both the sides of the equation and keep on dy/dx on the left hand side. This is because since our assumption was y equals xx, dy/dx would be equal to dxx/dx, and thus the derivative of the inner function would be xx ((ln x) + 1).
Then we differentiate the natural log and that gives us 1/xx. Now, as per the chain rule, we multiply the two derivatives and get the final result as follows:
d(ln xx)/dx = (1/xx) xx((ln x) + 1)
=> d(ln xx)/dx = ((ln x) + 1).
We multiplied the two derivatives as stated above and in the process cancelled out the xx from the denominator and the numerator. The answer we get hence is ((ln x) + 1).
Derivative of ln x½
Deriving the derivative of ln x½ is quite simple. It involves the differentiation of two very common functions, a logarithmic one and the other a simple variable. Let us start the process:
d/dx ln x½
= 1/x½ (d/dx x½)
= 1/x½ (-1/(2/x½))
= -1/2x.
The procedure is easy. The differentiation of the outer function, that is, the logarithmic function, gave 1/x½, and that of the inner function yielded (-1/(2/x½)). Then we simply multiply the two expressions and get the final answer as -1/2x.
Therefore, the derivative of ln x½ is -1/2x.
Derivative of ln x FAQs
How do you find the derivative of ln?
Finding the derivative of the natural logarithm of any function involves the consideration of the inner function first. If the inner function is simply, say, x, and it has to be differentiated with respect to itself, then the answer is just the reciprocal, that is, 1/x. However, if the function is a little different and complex, say x² or nx, then the differentiation is a little different but equally easy. We differentiate first the natural logarithmic function, and then multiply it with the derivative of the inner function. That will give us the desired answer, the derivative of the required natural logarithmic function.
What is the derivative of ln 2x?

The process to obtain the derivative of ln 2x is not much different from that for ln x. First, differentiate the natural logarithmic function and get 1/2x, the reciprocal of 2x, the internal function. Then differentiate the internal function 2x. The result will be 2. Lastly, multiply the two derivatives and get the final answer, the derivative of ln 2x. Follow the steps below:
d/dx (ln 2x)
= (1/2x) d/dx(2x)
= (1/2x) (2)
= 2/2x
= 1/x.
Therefore, the derivative of ln 2x is 1/x, exactly equal to the derivative of ln x.
What is integral of ln x?

The integral of ln x is xlnx – x + C.
It is given by
∫ln x dx
= xlnx – x + C, where C is an arbitrary constant.
What is 1 as a log?
The value of log 1 over log base 10 is zero (0).
It is easy to understand why. Follow the steps below:
100 = 1
=> log101 = 0.
10 raised to the power of zero is one. Then convert the expression to logarithmic form and get the answer.
How do you convert ln to log?
To convert natural log, that is, ln, to log base 10, multiply the natural log of the number with the log base 10 of e, that is, 2.71828. See the process below for more clarity:
log x = (ln x) (log 2.71828).